In the previous section we saw a simple example of a Frequency distribution table and also a Bar graph. Now we will see another example. This time the Class teacher of class VIII, Division C, wants to know the details about the heights (in cm) of the 32 students in that class.
The first step is to collect the raw data. As the students belong to a particular class, the heights can be collected in serial order, according to the roll number of the students. But even if it is collected in serial order, the data is 'raw' because the different heights will be distributed randomly in the list. The following list shows the raw data:
The Frequency distribution table and the Bar graph are shown in fig.1.9 below:
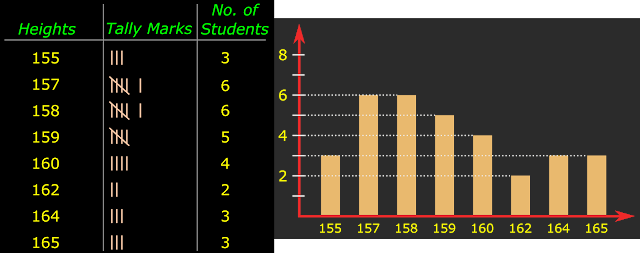 |
| Fig.1.9 Frequency distribution table and Bar graph |
The figs. self explanatory. We can see that 155 cm is the smallest height and 165 is the largest height. Six students have a height of 157 cm. Another six students have a height of 158 cm.
• In the above example, the data from a single division of class VIII was considered. So the raw data list is small.
• The values in the raw data list are close to each other. 155 is the smallest value and 165 is the largest value.
• There are values in between these two. There are 6 'in between values'.
• So there are a total of 8 values. Thus there are 8 rows in the Frequency distribution table, and there are 8 bars in the Bar graph.
• Also note that the values like 157, 158, 159 etc., repeated several times. So many 'tally marks' were accommodated into those rows.
Because of these properties, we obtained a small Table and a small Bar graph. In some cases we get a list of raw data with a large number of values.
• The values may not be close to each other. For example, one value may be 52, another may be 300, and yet another 520.
• There may be a vast difference between the smallest and the largest value. For example, the smallest may be 45 and the largest may be 580.
• As the list is large, the number of 'in between values' will also be large.
• If there are not many largely repeating values among these 'in between values', we will have to provide a large number of rows in the table. There will also be a large number of bars in the Bar graph.
In such situations, we divide the list into 'groups'. For example, suppose there are a total of 360 values in the raw data.
• If we decide to form groups, each with 20 values, the total 360 values will become 18 groups.
• If we decide to form groups, each with 40 values, the total 360 values will become 9 groups.
Thus we see that the large number of values are made into small number of manageable values. Now the question arises: How to form these groups?
The simplest way may seem to make the first 20 into the first group, the next 20 into the second group and so on. But such a grouping will not be of any help in 'analysing' the data. The raw data will still be 'raw'. We need a more 'scientific' method.
We can think of grouping based on 'similarity in properties'. That is., all the members of a group will be having similar properties. This can be explained with the help of an example. Suppose that there are 360 items in a raw data list. The items are the Electricity bill amount collected from 360 houses in a town in a particular month. [All the bills should be of a particular month. This is because, the electricity consumption in summer months will be greater than in winter months due to the usage of cooling appliances. If we collect the bill from some houses in a summer month, and some others in a winter month, the actual consumption of the whole town cannot be analysed] We want to divide the 360 items into groups. We want to do the division based on 'similarity in properties'.
This can be done as follows: The amounts which are close to each other should come in a group. For example, if a value in a group is 142, the other values that come in the group should be those like 120, 135, 160 etc., Other extreme values like 20, or 450 should not come in the group. 20 and 450 should fall into other appropriate groups. Let us see how this can be done:
We know the 'Number line'. A line in which the counting numbers are arranged in sequential order. The positive portion of it starts from the minimum value of zero, and can go up to any maximum value. This is shown in the fig.1.10 below:
 |
| Fig.1.10 Number line from zero to 8 |
Because of the limitation in space, we can show only upto 8 or 9. But this can be solved by changing the 'scale'. Thus, here is another number line which shows upto 80:
 |
| Fig.1.11 Number line from zero to 80 |
In fig.1.10, one unit represents '1'. But in fig.1.11, one unit represents '10'. In this way we can assume that one unit represents '50' or '100' to show up to 500 or 1000 in a small space.
So now we know about the Number line. Each of the values in the raw data list will fall onto a unique place in the Number line. Now, we divide the number line into equal intervals. This division can be done in many ways. One way is equal intervals of 20. Then, the intervals will be: 0 - 20, 20 – 40, 40 – 60, 60 – 80 etc., This is shown in the fig below:
 |
| Fig.1.12 Equal intervals of '20' on the Number line |
• Lower values will find their final places in any one of the intervals towards the left of the number line.
• Higher values will find their final places in any one of the the intervals towards the right of the number line.
So this is a scientific method of grouping. In the table shown in fig.1.9, which we saw earlier above, a row is assigned to every single value in the raw data list. (If a value repeats more than once, it need to be shown in one row only. Even then, for large data lists, the number of rows will become very large)
But in the above method, the 'intervals' take the place of 'values'. So the number of rows will become small. Once the first column of the table is filled up with the appropriate intervals, 'tally marking' can begin. We will see an example:
Given below is a raw data list of electricity bills of a particular month collected from 38 houses in a locality.
Let us prepare the Frequency distribution table. The smallest entry in the raw data list is 74. The largest entry is 389. So we want the portion from 74 to 389 in the number line. This is shown in the fig.1.13 below:
 |
| Fig.1.13 Portion from 74 to 389 |
• The 'length' of this red portion is 389 -74 = 315
• We want equal intervals in this red portion. Let us try to obtain 10 equal intervals. Then each interval will be 315/10 =31.5
• It is not convenient to mark equal intervals at 31.5. We must try to use multiples of 2, 5, 10, 50 or 100. The closest multiple to 31.5 is 50.
• So we will divide the red portion into equal intervals of 50
• The division of the red portion in this manner should coincide with the divisions on the number line also.
Based on the above, we will get the arrangement as shown below:
 |
| Fig.1.14 Equal divisions inside the Required portion |
So, instead of 10, we have obtained 7 equal intervals. We can now prepare the Frequency distribution table. We will see this in the next section.



No comments:
Post a Comment